量子蒙特卡洛(Quantum Monte Carlo, QMC)是解决量子问题的蒙特卡洛方法,分为变分蒙特卡洛(Variational Monte Carlo, VMC)、扩散蒙特卡洛(Diffusion Monte Carlo, DMC)等。
如果我们想要得到某个复杂体系的波函数与能量本征值,根据量子力学变分法有基态能为
\( E=\cfrac{\langle \Psi |\hat{H}|\Psi \rangle}{\langle \Psi |\Psi \rangle} \)
\( E=\cfrac{\int{\Psi ^*\left( R \right) \hat{H}\Psi \left( R \right) dR}}{\int{\left| \Psi \left( R \right) \right|^2dR}} \\ \quad=\cfrac{\int{\left| \Psi \left( R \right) \right|^2\Psi ^{-1}\left( R \right) \hat{H}\Psi \left( R \right) dR}}{\int{\left| \Psi \left( R \right) \right|^2dR}} \)
将其转化为
\( E\approx \cfrac{1}{M}\sum_i{E_{loc}\left( R_i \right)} \\ E_{loc}\left( R_i \right) =\Psi ^{-1}\left( R_i \right) \hat{H}\Psi \left( R_i \right) \)
即蒙特卡洛方法承认的形式。然后利用Metropolis方法得到样本。
\( \cfrac{P(x^{\prime})}{P(x)}=\left| \cfrac{\langle x^{\prime}|\Psi \rangle}{\langle x|\Psi \rangle} \right|^2 \)
\( A\left( x^{\prime}\gets x \right) =\min \left( 1,\cfrac{T\left( x\gets x^{\prime} \right) P\left( x^{\prime} \right)}{T\left( x^{\prime}\gets x \right) P\left( x \right)} \right) =\min \left( 1,\cfrac{P(x^{\prime})}{P(x)} \right) \)
之后计算基态能量。
另外,如果我们在希尔伯特空间有一组基,那么还可以求解
\( E=\cfrac{\sum_x{\left| \Psi \left( x \right) \right|^2\frac{\langle x|\hat{H}|\Psi \rangle}{\langle x|\Psi \rangle}}}{\sum_x{\left| \Psi \left( x \right) \right|^2}} \)
即
\( E=\cfrac{1}{N}\sum_{n=1}^N{E_{toc}\left( x_n \right)} \\ E_{loc}=\cfrac{\langle x|\hat{H}|\Psi \rangle}{\langle x|\Psi \rangle}=\sum_{x^{\prime}}{\langle x|\hat{H}|x^{\prime}\rangle \cfrac{\langle x^{\prime}|\Psi \rangle}{\langle x|\Psi \rangle}} \)
但我们依然不知道波函数的具体形式\(\Psi(R)\),因此需要取试探函数\(\Psi_{\tau}(R)\),其满足
\( E=\cfrac{\int{\left| \Psi _{\tau}\left( R \right) \right|^2\frac{\hat{H}\Psi _{\tau}\left( R \right)}{\Psi _{\tau}\left( R \right)}dR}}{\int{\left| \Psi _{\tau}\left( R \right) \right|^2dR}}\geqslant E_0 \)
有了试探波函数后,通过调整参数使得计算的基态能量逐步落到最小值,从而实现能谱计算。因此变分蒙特卡洛方法的精确度十分依赖于最初选取的试探波函数的形式。
变分蒙特卡洛的计算流程如下图
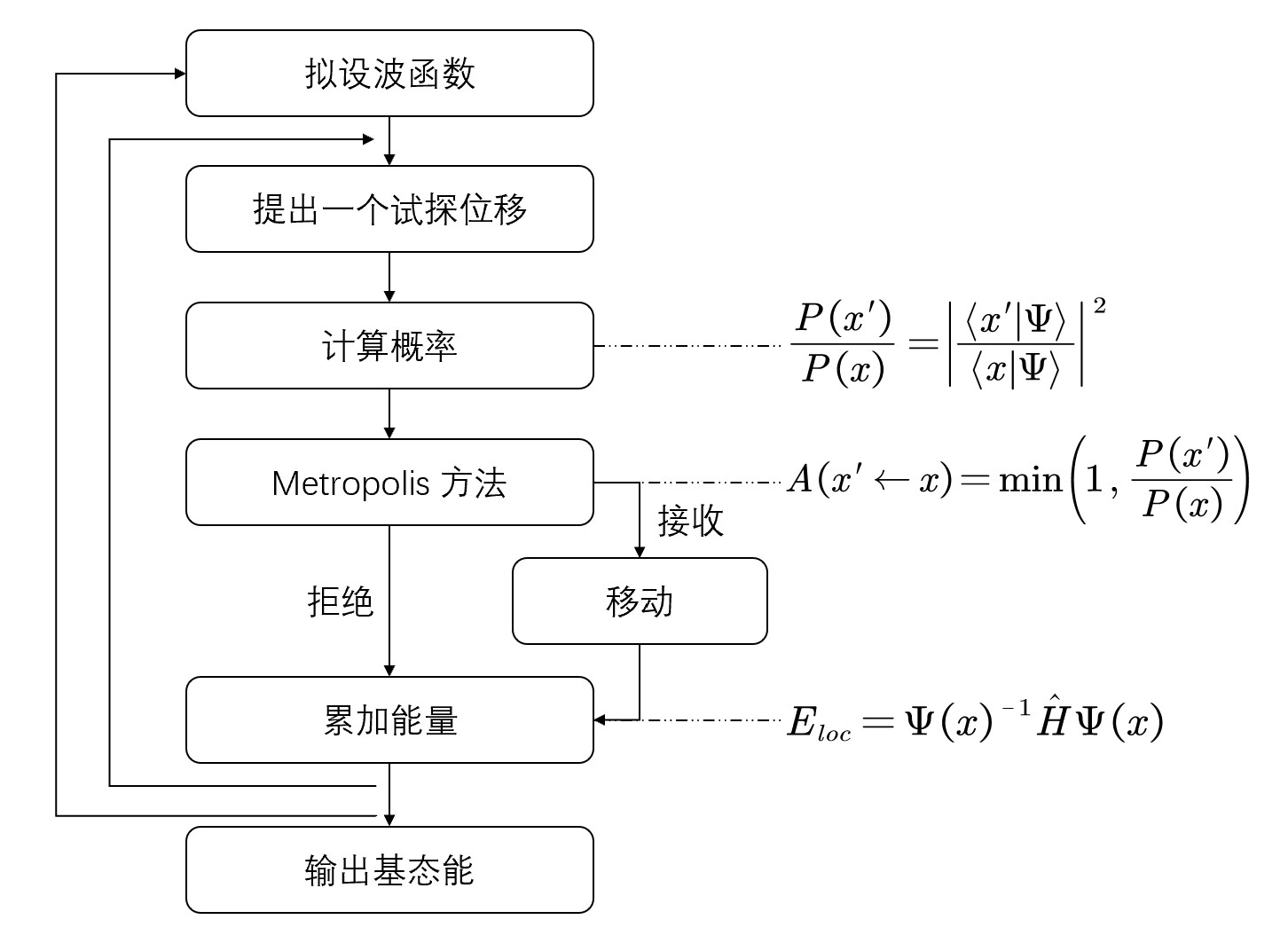
优化方法暂略
虚时演化法是一种本征态的数值计算求解方法,其具体做法是取任意一个随机试探波函数,使得这个波函数在虚时间下"反向"演化,从而回到一个低能本征态上。以下推导采用普朗克单位制。
含时薛定谔方程为
\( i\frac{\partial}{\partial t}\psi \left( \boldsymbol{r},t \right) =\hat{H}\psi \left( \boldsymbol{r},t \right) \)
定态薛定谔方程\(\hat{H}\phi _i\left( \boldsymbol{r} \right) =E_i\phi _i\left( \boldsymbol{r} \right)\),其中\(\phi _i\left( \boldsymbol{r} \right)\)为本征态,对应的本征能量为\(E_i\),有\(E_0 \leqslant E_1 \leqslant E_2 \leqslant ...\)
令虚时间\(\tau =it\),则含虚时薛定谔方程为
\( \frac{\partial}{\partial \tau}\psi \left( \boldsymbol{r},\tau \right) =-\hat{H}\psi \left( \boldsymbol{r},\tau \right) \)
先随机给定一个初始波函数\(\psi_{initial}(\boldsymbol{r},0)\),则可以写作本征态的叠加\(\psi _{initial}\left( \boldsymbol{r},0 \right) =\sum_i{c_i\phi _i\left( \boldsymbol{r} \right)}\)。则\(\tau\)时刻的波函数演化为
\( \psi _{initial}\left( \boldsymbol{r},\tau \right) =e^{-\hat{H}\tau}\psi _{initial}\left( \boldsymbol{r},0 \right) =\sum_i{c_ie^{-E_i\tau}\phi _i\left( \boldsymbol{r} \right)} \\ \qquad =e^{-E_0\tau}\left[ c_0\phi _0+\sum_{i=1}{c_ie^{-\left( E_i-E_0 \right) \tau}\phi _i\left( \boldsymbol{r} \right)} \right] \)
由于\(E_i-E_0 \geqslant 0\),随着\(\psi_{initial}(\boldsymbol{r},0)\)在虚时间下的演化,相较于\(\phi_0\),其他态会衰减地更快,最后只留下基态。
该方法也可以计算激发态,只需在计算过程中使波函数减去波函数在低能量态上的投影即可。
\( \exp \left( -\hat{H}\tau \right) =\sum_i{|\psi _i\rangle e^{-E_i\tau}\langle \psi _i|} \)
因此有
\( \lim_{\tau \rightarrow \infty} \langle \Psi \left( x \right) |e^{-\hat{H}\tau}|\psi _{initial}\rangle \\ =\lim_{\tau \rightarrow \infty} \sum_i{\langle \Psi \left( x \right) |\psi _i\rangle e^{-E_i\tau}\langle \psi _i|\psi _{initial}\rangle} \\ =\lim_{\tau \rightarrow \infty} \left( c_0e^{-E_0\tau}\langle \psi _0|\psi _{initial}\rangle +c_1e^{-E_1\tau}\langle \psi _1|\psi _{initial}\rangle +... \right) \\ \approx \lim_{\tau \rightarrow \infty} c_0e^{-E_0\tau}\langle \psi _0|\psi _{initial}\rangle \)
即初始波函数不断接近基态波函数时,其他项的权重迅速逐渐下降至接近零。
将哈密顿量分为动能项与势能项
\( \hat{H}=\hat{T}+\hat{V} \)
其中动能项为\(\hat{T}=-\frac{1}{2}\sum_i{{\nabla _i}^2}\),其本征方程为扩散方程
\( \cfrac{\partial \Psi \left( x,t \right)}{\partial t}=\cfrac{1}{2}\sum_i{{\nabla _i}^2\Psi \left( x,t \right)} \)
采用格林函数法求解,其格林函数为
\( G\left( x\gets x^{\prime},\tau \right) =\left( 2\pi \tau \right) ^{-\frac{3N}{2}}e^{-\frac{\left( x-x^{\prime} \right) ^2}{2\tau}} \)
在加上势能项,其格林函数可写作
\( G\left( x\gets x^{\prime},\tau \right) \approx \left( 2\pi \tau \right) ^{-\frac{3N}{2}}e^{-\frac{1}{2\tau}\left( x-x^{\prime} \right) ^2}\times e^{-\frac{\tau}{2}\left[ V\left( x \right) +V\left( x^{\prime} \right) \right]} \)
乘号后面的项可以看作权重。为了使得权重不太大(避免粒子数发散问题),可以采用以下操作将e指数上的能量减掉
\( -\cfrac{\partial \Psi \left( x,t \right)}{\partial t}=\left( \hat{H}-E_{\tau} \right) \Psi \left( x,t \right) \)
\( G\left( x\gets x^{\prime},\tau \right) \approx \left( 2\pi \tau \right) ^{-\frac{3N}{2}}e^{-\frac{1}{2\tau}\left( x-x^{\prime} \right) ^2}\times e^{-\frac{\tau}{2}\left[ V\left( x \right) +V\left( x^{\prime} \right) -2E_{\tau} \right]} \)
令\(P_{reweight}=exp[-\cfrac{\tau}{2}[V(x)+V(x')-2E_\tau]]\),则P可以被解释为"walker"克隆或者死亡的概率。"walker"在能级上不断向虚时间方向行走,最后到达\(\tau \rightarrow \infty\)的基态后形成一个分布,即为基态波函数。但"walker"可能会由于权重没有归一化而克隆或者死亡,造成计算结果点太少而导致统计误差较大(死的太多了)或者结果点膨胀而导致内存不足(克隆的太多了)。
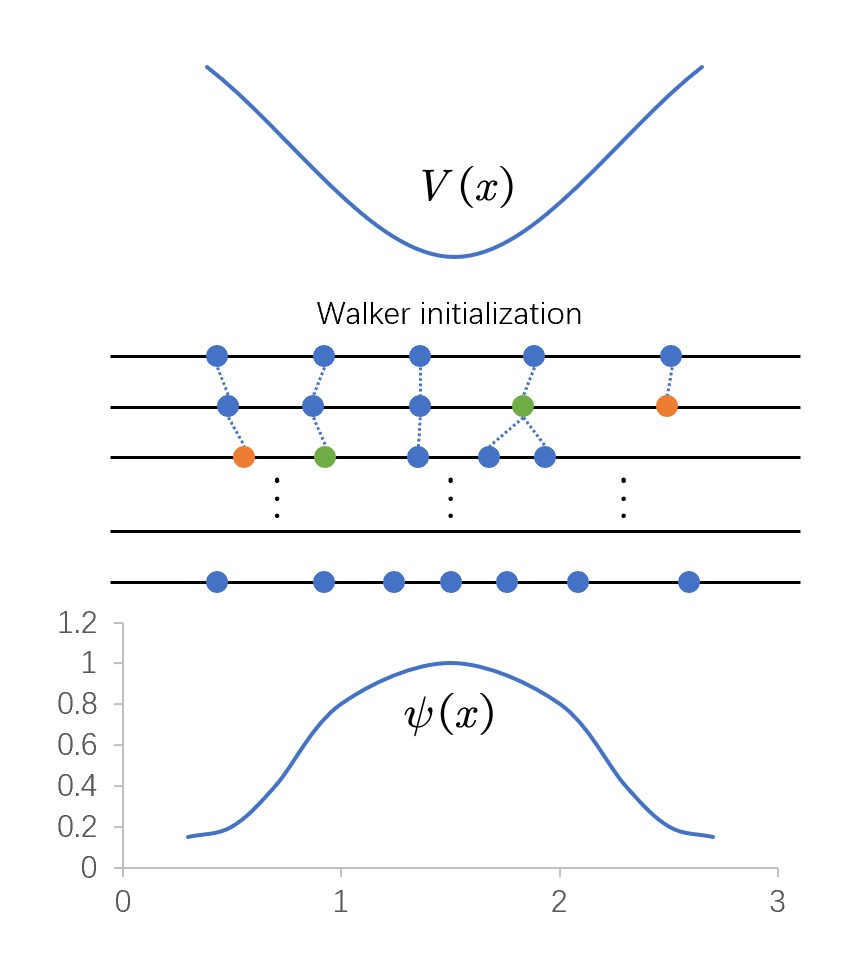
根据重要性采样思想,引入“引导波函数”\(\Psi_\tau(x)\)
\( -\cfrac{\partial \Psi \left( x,t \right)}{\partial t}=\left( \hat{H}-E_{\tau} \right) \Psi \left( x,t \right) \quad \rightarrow \quad -\cfrac{\partial \Psi \left( x,t \right) \Psi _{\tau}\left( x \right)}{\partial t}=\left( \hat{H}-E_{\tau} \right) \Psi \left( x,t \right) \Psi _{\tau}\left( x \right) \)
令\(f\left( x,t \right) =\Psi \left( x,t \right) \Psi _{\tau}\left( x \right) \),将其带入薛定谔方程
\( -\partial _tf\left( x,t \right) =-\frac{1}{2}\nabla ^2f\left( x,t \right) +\nabla \left[ v_D\left( x \right) f\left( x,t \right) \right] +\left[ E_L\left( x \right) -E_{\tau} \right] f\left( x,t \right) \)
\( v_D\left( x \right) =\nabla \ln |\Psi _{\tau}\left( x \right) |={\Psi _{\tau}}^{-1}\left( x \right) \nabla \Psi _{\tau}\left( x \right) \\ E_L\left( x \right) ={\Psi _{\tau}}^{-1}\left( x \right) \hat{H}\Psi _{\tau}\left( x \right) \)
其中\(v_D\)为引导"walker"向波函数增大的方向移动。
在DMC语言中,我们将\(f(x,t+\tau)\)使用格林函数法变为
\( f\left( x,t+\tau \right) =\int{\tilde{G}\left( x\gets x^{\prime},\tau \right) f\left( x^{\prime},t \right) dx^{\prime}} \)
其中
\( \tilde{G}\left( x\gets x^{\prime},\tau \right) \approx G_d\left( x\gets x^{\prime},\tau \right) G_b\left( x\gets x^{\prime},\tau \right) \\ G_d\left( x\gets x^{\prime},\tau \right) =\left( 2\pi \tau \right) ^{-3N/2}\exp \left[ -\cfrac{1}{2\tau}\left[ x-x^{\prime}-\tau v_D\left( x^{\prime} \right) \right] ^2 \right] \\ G_b\left( x\gets x^{\prime},\tau \right) =\exp \left[ -\cfrac{\tau}{2}\left[ E_L\left( x \right) +E_L\left( x^{\prime} \right) -2E_T \right] \right] \)
则接收概率为
\( P_{accept}=\min \left[ 1,\cfrac{G_d\left( x^{\prime}\gets x,\tau \right) G_b\left( x^{\prime}\gets x,\tau \right) \Psi _T\left( x \right) ^2}{G_d\left( x\gets x^{\prime},\tau \right) G_b\left( x\gets x^{\prime},\tau \right) \Psi _T\left( x^{\prime} \right) ^2} \right] =\min \left[ 1,\cfrac{G_d\left( x^{\prime}\gets x,\tau \right) \Psi _T\left( x \right) ^2}{G_d\left( x\gets x^{\prime},\tau \right) \Psi _T\left( x^{\prime} \right) ^2} \right] \)
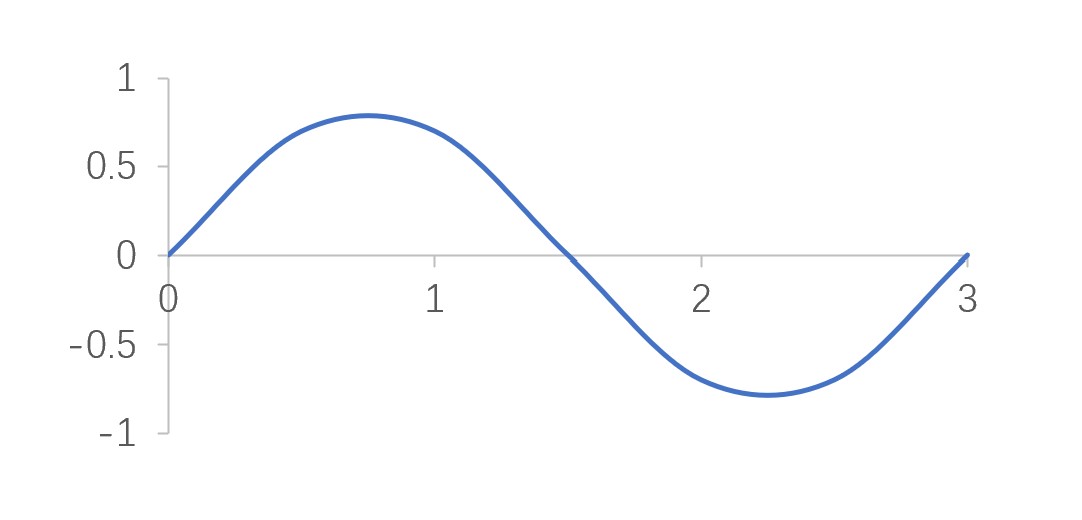
由于DMC方法对波函数进行演化,而并非其模方,因此在迭代过程中"walker"可能会掉入负半轴,并且在负半轴向更“小”的方向演进,从而造成误差过大。符号问题有多种解决办法,但效果都不好,主流办法是固定节点近似。

以波函数为0的区域为边界,将空间划分为“正空间”与“负空间”,使得"walker"不能穿过边界,从而限制"walker"的正负。
